• Метод Ньютона- Программа На Паскале

Метод Ньютона, реализованный на Паскале. // Метод Ньютона - метод второго порядка. Решение: Формулировка задачи: Метод Ньютона (касательных) - Pascal. Код к программе.

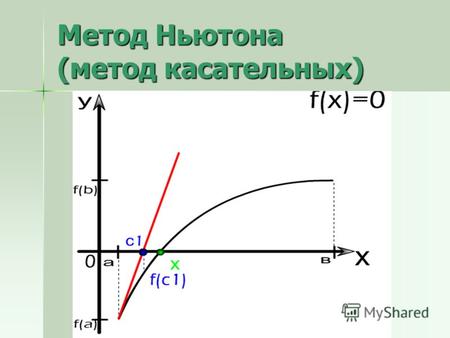
Теоретическая часть.4 3. Алгоритм работы.8 4. Код программы.17 Модуль Kgraph.17 Модуль Graphic.34 Модуль Kunit.38 Основная программа.40 5. Ключи на алавар. Драйвера на мышку x7 f6. Тестовые испытания.42 6. Полезные советы по работе с программой.42 7. Окна ввода и вывода программы. Вывод.43 9. Игры стратегии играть онлайн.

Список литературы.44. Математика -одна из самых древних наук. Труды многих ученых вошли в мировой фонд и стали основой современных алгебры и геометрии.

В конце XVII в., когда развитие науки шло быстрыми темпами, появились понятия дифференцирование, а вслед за ним и интегрирование. Многие правила нахождения неопределенного интеграла в то время не были известны, поэтому ученые пытались найти другие, обходные пути поиска значений. Первым методом явился метод Ньютона – поиск интеграла через график функции, т.е. Нахождение площади под графиком, методом прямоугольников, в последствии усовершенствованный в метод трапеций. Позже был придуман параболический метод или метод Симпсона. Однако часть ученых терзал вопрос: А можно ли объединить все эти методы в один??

Ответ на него был дан одновременно двумя математиками Ньютоном и Котесом. Они вывели общую формулу, названную в их честь. Однако их метод был частично забыт. В этой работе будут изложены основные положения теории, рассмотрены различные примеры, приведены таблицы, полученные при различных погрешностях, и конечно описана работа и код программы, рассчитывающей интеграл методом Ньютона-Котеса. Теперь произведем анализ алгоритма и рассмотрим основной принцип работы программы. Для вычисления интеграла сначала находятся коэффициенты Ньютона-Котеса. Их нахождение осуществляется в процедуре hkoef.

Основной проблемой вычисления коэффициентов является интеграл от произведения множителей. Для его расчета необходимо: А) посчитать коэффициенты при раскрытии скобок при q (процедура mnogoclen) Б) домножить их на 1/n, где n –степень при q (процедура koef) В) подставить вместо q значение n (функция integral) Далее вычисляем факториалы (функция faktorial) и перемножаем полученные выражения (функция mainint). Для увеличения быстроты работы вводится вычисление половины от количества узлов интерполяции и последующей подстановкой их вместо неподсчитанных.

Метод Ньютона- Программа На Паскале

Процедура koef(w: массив; n:целый; var e:массив).